Dovetail Angles – a trigonometric approach

I’m sure everyone knows by know that I’m just getting started in woodworking and in prepping to cut my first dovetails I became curious just what the common dovetail angles turn out to be. I showed you my prototype dovetail markers last time the first a 1:8 and the second a 1:6 marker. For that exercise I used graph paper to draw the angles, then took my sliding bevel to transfer the angle to my wood on the first marker. On the second one, I cut out a paper template and glued it to the wood. I was curious why few folks mention the actual angles these slopes represented. Of course the answer was “out there” but I wanted to calculate them myself  as an exercise.

Digging deeply into my high-school-trig-knowledge-brain-base I vaguely remembered that given a right triangle I could calculate the included angle if I knew the opposite and the adjacent side lengths. I wasn’t exactly sure but a quick search brought up the refresher information I needed.

So to calculate the angle x in the above figure we need to take the inverse tangent (also called the arc tangent) of the opposite side (O) divided by the adjacent side (A) of the triangle. So in the case of my first 1:8 marker I need the angle to be:

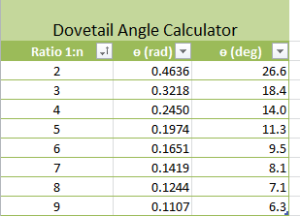
x=arctan(1/8) = 0.1244 radians

Right that is another complication. To refresh our memories once again, a circle is comprised of 360° which is the equivalent of  2π radians (2 times pi).  The irrational number Pi can be approximated as the value 3.14.  Thus the following holds:

x°= 0.1244 rad * (180° / 3.14 rad) =  7.12°

So there you have it, a 1:8 dovetail angle represents about 7°. Here’s a table I whipped up in Excel with more angles.

This dovetail angle calculator is available for those that might have an interest in looking under the covers.

In summary, from my reading it is clear the actual angles really don’t matter very much and here’s a few arguments why.

1. It’s fairly difficult to see the difference between a 1:6 and a 1:8 dovetail angle unless you are trained and even then you’d measure to be sure.
2. There really isn’t that much structural difference either. Many claim the soft wood (1:8) versus hardwood (1:6) recommendation has little merit and opt for a single angle which is sometimes 1:7 for all joints.
3. Some claim if you’re going to cut dovetails you might as well make them “look like dovetails” and so they use a more pronounced angle to show them off, often 14° is mentioned which turns out to be approximately 1:4
4. A tails don’t necessarily have to be the same width on a tail board. In theory you could have pins with different angles within the same joint but I’m not sure if folks experiment much with this, I’m merely speculating.
5. No one cares what the angle is but some might notice if one side  of the pin is different from the other, so symmetry seems like it is important at least on a pin for pin basis.

So we all agree, no one should really care that much about absolute angles I just wanted tie together some of the tidbits of information I had been collecting from all the place. If this was a post on brewing I’d use the home brewer’s mantra, “relax have a home-brew”. In this case I’ll say, “enjoy your time in the shop and remember math is fun!”.

You have been reading an excerpt from the shop journal of the Turtlecovebrewer.